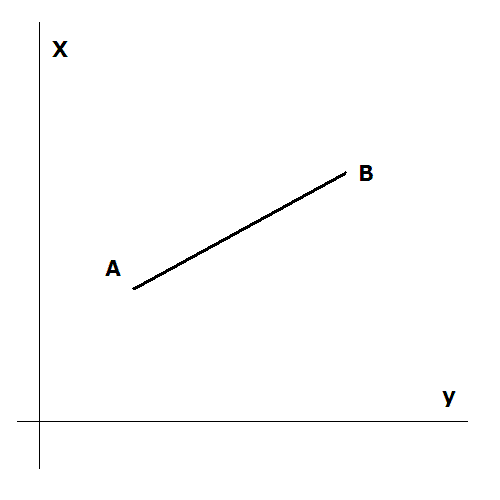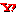Vienas kolega manęs užklausė, kaip, turint sklypo kampų GPSu išmatuotas koordinates LKS-94 sistemoje, nustatyti linijos ilgį. Pamąsčiau, kad gal kam tas irgi praverstų, tai toks viešas atsakymas
Visų pirma, reikia žinoti, kad LKS-94 (1994ųjų metų Lietuvos Koordinačių Sistema, jei norėsite gūglinti ar šiaip) koordinačių ašys X ir Y sukeistos vietomis 😉
Dabar apie pačią problemą:
Turime du taškus (A ir B) su nustatytomis (plokščiomis stačiakampėmis) koordinatėmis X,Y: A(
XA,
YA) ir B(
XB,
YB) LKS-94 koordinačių sistemoje. Kaip taisyklė, jos nustatomos metrais, skirtingai nuo kai kada GPS rodomų WGS-84 World Geodetic System of Year 1984) geodezinių/geografinių koordinačių B,L (platumos, ilgumos), kurios nustatomos laipsniais-minutėmis-sekundėmis
Reikia paskaičiuoti linijos ilgį
S tarp šių taškų. Galbūt, kai kurie gudrūs GPS leidžia tą padaryti, bet kai turime tik pačias koordinates – joks GPS nepadės, tik kalkuliatorius
Taigi, visų pirma skaičiuojame koordinačių skirtumus:
DXAB=
XB-
XA
DYAB=
YB-
YA
Tada skirtumus pakeliame kvadratu ir sudedame:
DXAB*2+
DYAB*2=
S2
Linijos ilgis bus kvadratinė šaknis iš S2:
S=sqrt(
S2)
UPD. Vienas iš G+ komentatorių uždavė klausimą, o kaipgi su aukščių skirtumais linijos galuose, dėl kurių išmatuota vietovėje linija visad trumpesnė už atvaizduotą žemėlapyje. Tai va, tokiu atveju reikia įvesti pataisą už aukštį:
Kokiu nors būdu (iš žemėlapio, iš GPS parodymų) nustatome linijos galų A ir B aukščius virš jūros lygio metrais: A(
HA) ir B(
HB)
Skaičiuojame aukščių skirtumą:
DHAB=
HB-
HA
Tada aukščių skirtumą pakeliame kvadratu ir daliname iš dvigubo linijos ilgio
S:
DHAB=
DHAB*2/2*
S
Pataisome išmatuotą linijos ilgį – gauname
linijos ilgį žemėlapyje:
Spataisytas=
S–
DHAB
Kada tos pataisos reikia? Viskas priklauso nuo reikalaujamo tikslumo – pvz, 100m atsumu, jei aukščių skirtumas 1m – pataisa 0.5cm; tuo pačiu 100m atstumu, jei aukščių skirtumas 2m (virš žmogaus ūgio, tą galima „iš akies“ nustatyti) – 2cm. Taip kad jei kažką matuojate sprindžio (~15cm) tikslumo – vargu bau prisireiks 😉